Fitting method

For the two disk (thin+thick) model fitting with four parameters, in the 1D case, is complicated; fitting with six parameters as in the 2D case, is even more complex. The main problem is that a fitting model with so many free parameters can obtain many possible solutions to give a good fit. Determining which fit result is the best can not be put to guessing, especially when one searches for the lowest 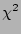$\chi^2$ value, following the formula

$$\chi^2\ =\ \sum \textrm{(data\ -- model)}^2\ .$$ (14)

The typical methods use the Levenberg-Marquardt least-squares algorithm for fitting. Just for the one dimensional model, with only four parameters, the fitting results with this algorithm are already highly inconclusive, giving many possibilities. The 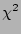$\chi^2$ value differences are minimal. Varying along a large range of solutions only provides long computation times and leads to an other solution than the input values. The least-squares algorithm only looks for low 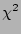$\chi^2$ values in the neineighbourhoodhereas one wants to look around a range of boundaries for the region that shows the steepest slope to a solid 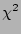$\chi^2$ solution.
A method that meets these requirement better is the Downhill Simplex method [Nelder and Mead1965]. This method variates the searching area for the best fit according to a set of boundary values, variating the search area in shape and size to find the lowest 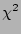$\chi^2$ value, after which it shrinks the boundary area to the parameter values of this 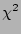$\chi^2$ value, setting them as the input parameters. It repeats the process until it returns the input parameters of the lowest 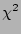$\chi^2$ value it had found. Not only converges this method much faster than the least-squares fit, it is easily extendable when adding more parameters, as needed for the 2D case, and it is able to really converge to a final solution.