Starting values for the Downhill-Simplex method

The least-squares fit showed us that many combinations of the 4 parameters of the two disk fitting function are possible to provide an acceptable fit. Even the Downhill Simplex method has troubles when there are few datapoints for a fitting function with many free parameters or the datapoints show great irregularity.
The Downhill Simplex method requires one to input several sets of starting values in an array which the algorithm will use as boundaries for its fitting area in which it will search for the smallest differences between the datapoints and the model fit function. The parameter space can become huge with many parameters being allowed to vary over a large range. To decrease computation time and make sure the fit gives acceptable results, boundaries have to be set to the parameter space in which the method will search for the lowest 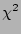$\chi^2$ value. For this the input parameters have to be narrowed down before the actual fitting begins.
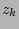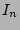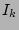Narrowing down the starting values is most important for the vertical profiles. $z_n$ and $z_k$ determine the slope of the two disk components as each describe two different regions of the profile. These values can vary freely between steep and flat if one does not put constraints to this freedom. 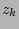This can be done by putting a boundary on the values for $I_n$ and $I_k$ who limit how faint or bright the thin and the thick can become in the center of the galaxy, constraining the values $z_n$ and $z_k$ can obtain. 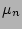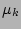For the fit we use the surface brightnesses, $\mu_n$ and $\mu_k$, in mag arcsec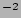$^{-2}$, as input, which are converted into luminosities for the input parameters, because the surface brightness values show the difference better than the larger or smaller luminosity values.
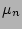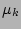As we are limited by how deep our galaxy images reach, the difference between $\mu_n$ and $\mu_k$, which we will address henceforth as 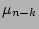$\mu_{n-k}$, is limited for the typical 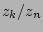$z_k/z_n$ ratios. 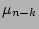$\mu_{n-k}$ cannot be too large, as the thick disk will be too faint to be distinguished from the background noise, and not too small, because in that case the thick disk will be too bright and either dominate the profile or be indistinguishable from the thin disk. We have set these two extreme cases, and outer limits, at 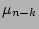$\mu_{n-k}$ = 2 and 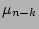$\mu_{n-k}$ = 6 mag arcsec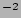$^{-2}$. So the expected values for 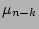$\mu_{n-k}$ should be between 3 and 5 mag arcsec$^{-2}$.
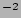The value of 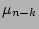$\mu_{n-k}$ is however not something one can easily allow to vary in the Downhill Simplex method. We tried to use the intermediate 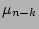$\mu_{n-k}$ value of 4 for our fits, but this did not result in a free variation of 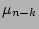$\mu_{n-k}$ and constrained 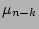$\mu_{n-k}$ and the other starting values too much. Although it was able to always fit the profile and converge to acceptable values, those results were not satisfying as 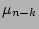$\mu_{n-k}$ only changed in some cases.
The only solution to this was to release the constraints on 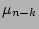$\mu_{n-k}$ and allow a full parameter range for the fits. However, we still wanted to keep the parameter space small to narrow down on the correct and best solution. To constrain the input parameters we determined them from the actual profile data. We made a sequence of simple linear fits, on the datapoints of the first cut, for the thin and the thick disk, shifting in the 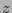$z$-direction with steps to obtain a range of magnitude and scaleheight values. The most extreme cases were combined to make an additional worst case input set of parameter values to allow the Downhill Simplex method to go search further out for possible solutions. Figure 6 shows an example of this method on the first profile cut of NGC 5290 J. The fits with the same colour in the inner and the outer part represent the thin and thick disk starting values respectively.
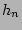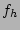$h_n$ and $f_h$, which are described by a single function, were given a typical range of values for were put into a list, 15-45 and 0.5-3.0 respectively, and separately randomly added to the thin and thick disk starting values.
For some of the sample galaxies we put in an extra constraint if possible. From the radial bulge part three equipositioned cuts were selected and from those the datapoints were taken that were clearly outside the bulge and describing a vertical structure component.

Figure 6: Linear fits to the inner and the outer regions of a profile of NGC 5290 J to create starting values for the Downhill Simplex method. Each combined inner and outer region fit lines have the same colour.