Binning

Binning, which is the grouping of datapoints and taking the average value of them, is incredibly important when fitting surface brightness profiles.
To attest the highest quality to a fit one would like to use as much of the observed surface brightness profile as possible. For one dimensional fits we used the original galaxy image, which includes many variations and irregularities for each vertical profile. The quadrasized average smoothens the surface to some extent and also increases the S/N ratio, but not sufficiently.
Binning itself smoothens the surface brightness to some extent, depending on its size, but it does not take into account that at lower surface brightness areas, at higher vertical and larger radial positions, the S/N ratio will go down and more area has to be taken into the bin for sufficient smoothing.
To solve this issue one makes the binsizes grow vertically and radially to improve the profile even more, as one desires to follow the vertical structure as far out as possible and to keep the S/N ratio almost constant for all points in the inner and outer part, because that will improve the quality of the fit. The minimum bin is equivalent to the FWHM, 3 pixels. The growing goes according to the function

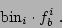$$\textrm{bin}_i \cdot f_b^{i}\ .$$ (13)

The growing factor 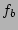$f_b$ is very important. This factor can make the bins smaller and larger per radius and 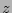$z$ depending on its value. The factor cannot be too small, or it would not smoothen the irregularities sufficiently, and it cannot be too large, as it would smoothen and flatten the profile too much as it takes too much area into the average. A too large 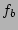$f_b$ also decreases the number of cuts that can be used for the fit as the bins grow larger but the selected radial fit region keeps the same size. The effects of changing the 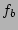$f_b$ value on the amount of datapoints varies. As datapoints are lost due to less cuts, it is able to obtain more datapoints vertically because the bin takes more datapoints into its average. Tests on the shape of the profiles showed a 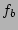$f_b$ of 1.07 to be, in our case, a minimum for smoothening sufficiently to obtain a successfull fit. From this number only small increases in the trend of 0.01 already improves the profiles considerably, but also quickly takes effect on the amount of cuts.
As an example, figure 5 shows the central positions of all the bins in the vertical and radial direction, with 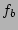$f_b$ is 1.09, on the upper north-east quadrant of the image of NGC 5290 J.

Figure 5: Example of a grid on NGC 5290 J, showing the central positions of the bins which grow in size with a factor of 1.09 in the vertical and the radial direction in one quadrant.