



Next: Conclusions
Up: Vertical colour profiles &
Previous: Determining colour gradients
Contents
Results & discussion
Plots of the colour profiles for each of the six galaxies and their selected profiles for the gradient fit are shown in Appendix C, together with the single gradient fit results at their respective radii for each of the six galaxies in the tables A to F.
Two single stellar population models with different metallicity and initial mass functions are used to determine the properties of our colour profiles. The details are shown in table 18, which is adapted from the GALAXEV manual (2003), which can be downloaded from the GALAXEV website9, and shows the metallicities of the SSP of the Bruzual & Charlot population synthesis models [Bruzual and Charlot2003]. The models were computed using the Chabrier chabrier2003 IMF with lower and upper mass cutoffs at 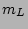 = 0.1
= 0.1 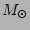 and
and 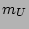 = 100
= 100 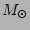 respectively. The SSP models are normalized to a total mass of 1
respectively. The SSP models are normalized to a total mass of 1 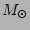 in stars at age
in stars at age 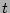 = 0.
= 0.
For a better comparison of the results the Vazdekis population synthesis models10 were used as well. The models were computed using the Unimodal Salpeter IMF with lower and upper mass cutoffs at 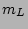 = 0.01
= 0.01 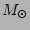 and
and 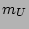 = 200
= 200 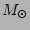 respectively, whereas the faintest star is 0.09
respectively, whereas the faintest star is 0.09 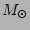 . The Vazdekis models use a smaller range of metallicities but also smaller intermediate steps. For more details see Vazdekis et. al vazdekis1996.
. The Vazdekis models use a smaller range of metallicities but also smaller intermediate steps. For more details see Vazdekis et. al vazdekis1996.
TABLE 18
M
ETALLICITIES OF THE B
RUZUAL-C
HARLOT SSP
MODELS
Key |
Z |
X |
Y |
[Fe/H] |
| m22 |
0.0001 |
0.7696 |
0.2303 |
-2.2490 |
| m32 |
0.0004 |
0.7686 |
0.2310 |
-1.6464 |
| m42 |
0.004 |
0.7560 |
0.2400 |
-0.6392 |
| m52 |
0.008 |
0.7420 |
0.2500 |
-0.3300 |
| m62 |
0.02 (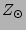 ) ) |
0.7000 |
0.2800 |
+0.0932 |
| m72 |
0.05 |
0.5980 |
0.3520 |
+0.5595 |
Notes:  Padova 1994 evolutionary track; see Bruzual & Charlot bruzual2003 for references. The key names the list for each set of metallicities. X, Y, Z are the fractional abundances of hydrogen, helium and everything else, respectively. Padova 1994 evolutionary track; see Bruzual & Charlot bruzual2003 for references. The key names the list for each set of metallicities. X, Y, Z are the fractional abundances of hydrogen, helium and everything else, respectively. |
Table 19 shows in columns 2 and 3 the average gradients for the respective galaxies. The gradients are presented in mag arcmin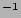 and mag
and mag 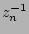 . The average gradient (
. The average gradient (
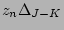 ) is -0.063
) is -0.063  0.027 mag
0.027 mag 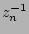 . The (
. The ( ) in column 4 is not corrected for the galactic extinction. The average (
) in column 4 is not corrected for the galactic extinction. The average ( ) value, corrected for the galactic extinction, is 0.962
) value, corrected for the galactic extinction, is 0.962  0.066 magnitude.
0.066 magnitude.
To determine qualitative insight into the results of our gradient fits we applied them to the Bruzual-Charlot and Vazdekis models to derive what kind of stellar populations we find at different vertical heights and if our results are viable. To determine the tracks for the inner and outer vertical height a single stellar population with an age of minimal 15 Gyr was selected to cover the oldest stars in the galaxy. For those ages the resulting ( ) for the gradient position was compared to the metallicity tracks of the Bruzual & Charlot and the Vazdekis models.
) for the gradient position was compared to the metallicity tracks of the Bruzual & Charlot and the Vazdekis models.
Both models have their advantages and disadvantages. The Bruzual & Charlot models have a larger range in metallicities and hence in ( ) values, while the smaller steps between metallicities in the Vazdekis models allow a more accurate determination of the metallicity, although this does not go up at extreme values.
) values, while the smaller steps between metallicities in the Vazdekis models allow a more accurate determination of the metallicity, although this does not go up at extreme values.
Table 20 shows the different metallicities according to the average gradients for each galaxy taking 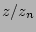 = 0 and
= 0 and 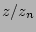 = 4 for the inner and outer vertical heights, as most selected profiles are not able to reach much further out, to determine their population properties. For this the (
= 4 for the inner and outer vertical heights, as most selected profiles are not able to reach much further out, to determine their population properties. For this the ( ) gradient difference from the two positions was subtracted from the average (
) gradient difference from the two positions was subtracted from the average ( ) of the fit, which value is equal to the central value at
) of the fit, which value is equal to the central value at 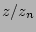 = 0. The median abundance gradient is -0.049
= 0. The median abundance gradient is -0.049 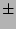 0.18
0.18 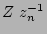 . The median is taken as IC 3322A gives a value of -0.006 and NGC 0973 -0.028, while the other values are equal at 0.049. Their low values originate from a low overall (
. The median is taken as IC 3322A gives a value of -0.006 and NGC 0973 -0.028, while the other values are equal at 0.049. Their low values originate from a low overall ( ) and a rather flat gradient, respectively.
) and a rather flat gradient, respectively.
All galaxies show high metallicities in the mid plane while IC 2531 and UGC 4277 show values above the model possibility. This unusual high value can be contributed to reddening by dust extinction as both galaxies possess prominent dustlanes and are about perfectly edge-on. Thus the correct gradients for IC 2531 and UGC 4277 are probably smaller. As the high metallicity for the inner part is expected and the ( ) values remain within model values, the influence of dust is probably small in our fit. The outer parts show in all cases lower metallicities.
) values remain within model values, the influence of dust is probably small in our fit. The outer parts show in all cases lower metallicities.
TABLE 20
M
ETALLICITIES FOR 15 G
YR S
TARS ON G
RADIENTS
As we found that ( ) gives insight in the metallicity of the stellar population, the models also allow us to see if we can gain insight in the age of the stellar population over vertical height. We did this by determining the stellar population ages of stars with a solar metallicity (m62) and with a minimal age of 1 Gyr. We expected not to be able to get results and this was also the case. Thus we can confirm that (
) gives insight in the metallicity of the stellar population, the models also allow us to see if we can gain insight in the age of the stellar population over vertical height. We did this by determining the stellar population ages of stars with a solar metallicity (m62) and with a minimal age of 1 Gyr. We expected not to be able to get results and this was also the case. Thus we can confirm that ( ) colour profiles are a good indicator for change in the metallicity of stellar populations, but weak on changes in the stellar population ages, as James et. al (2006) state.
) colour profiles are a good indicator for change in the metallicity of stellar populations, but weak on changes in the stellar population ages, as James et. al (2006) state.
To be able to compare our results with those from De Grijs & Peletier (2000), we converted each average ( ) gradient to a (
) gradient to a (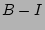 ) gradient. This was done by selecting the same age for the model (15 Gyr) and matching it with the metallicity models that we had found for the (
) gradient. This was done by selecting the same age for the model (15 Gyr) and matching it with the metallicity models that we had found for the ( ) values, to determine the (
) values, to determine the (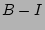 ) values for these metallicities. From this a
) values for these metallicities. From this a
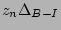 gradient could be determined. The median (
gradient could be determined. The median (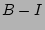 ) colour at
) colour at 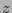 = 0 is 2.56
= 0 is 2.56 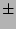 0.23 magnitude for the Bruzual-Chabrier models and 2.41
0.23 magnitude for the Bruzual-Chabrier models and 2.41 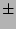 0.19 magnitude for the Vazdekis models. The resulting gradients are shown in Table 19. The average (
0.19 magnitude for the Vazdekis models. The resulting gradients are shown in Table 19. The average (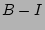 ) gradient is -0.150
) gradient is -0.150 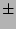 0.072 mag
0.072 mag 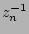 for the Bruzual-Charlot models and -0.109
for the Bruzual-Charlot models and -0.109 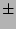 0.069 mag
0.069 mag 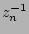 for the Vazdekis models. The slightly lower Vazdekis values are caused by its lower extremes for possible high or low (
for the Vazdekis models. The slightly lower Vazdekis values are caused by its lower extremes for possible high or low ( ) and (
) and (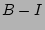 ) values, which automatically leads to smaller gradients. Thus we consider the Bruzual-Charlot models to be better in our case as our values remain better within their extremes than the Vazdekis models.
) values, which automatically leads to smaller gradients. Thus we consider the Bruzual-Charlot models to be better in our case as our values remain better within their extremes than the Vazdekis models.
We find that our gradient is not only blueing but also much larger than the De Grijs & Peletier (2000) result of 0.03 or their alternative gradient of 0.06 from a model with a different star formation rate. On average, the earlier-type galaxies of De Grijs & Peletier (2000), exhibit smaller vertical (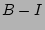 ) gradients than the later types, but their (
) gradients than the later types, but their (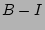 ) gradients are not as large as our (
) gradients are not as large as our (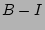 ) gradients, showing their gradients are influenced by star formation close to the plane. Evenso, the observation of a blueing of the galactic disk with height above the plane cannot always rule out the possibility that this is due to extinction effects while the center part is reddened by dust. However, since almost all of our profiles show a blueing trend in the gradient of which some are quite strong, they cannot all be simply explained by these effects, as our inner part values remain within model values and can be assigned to a higher metallicity.
) gradients, showing their gradients are influenced by star formation close to the plane. Evenso, the observation of a blueing of the galactic disk with height above the plane cannot always rule out the possibility that this is due to extinction effects while the center part is reddened by dust. However, since almost all of our profiles show a blueing trend in the gradient of which some are quite strong, they cannot all be simply explained by these effects, as our inner part values remain within model values and can be assigned to a higher metallicity.
A comparison with Dalcanton & Bernstein (2002) is more difficult, as they do not provide colour gradients for their (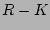 ) profiles. Our sample galaxies are also all high-mass galaxies, so we cannot say anything about their low-mass results. They assign their reddening in the inner part of the colour profiles of their high-mass galaxies to dust. In our case, as we have taken the side where there is no dustlane and went further out for the gradient fit to avoid its effects, we cannot say the same thing. As the central (
) profiles. Our sample galaxies are also all high-mass galaxies, so we cannot say anything about their low-mass results. They assign their reddening in the inner part of the colour profiles of their high-mass galaxies to dust. In our case, as we have taken the side where there is no dustlane and went further out for the gradient fit to avoid its effects, we cannot say the same thing. As the central ( ) values remain within model values for stars with high metallicity in the inner part and low metallicity in the outer part this means that dust is probably not dominating the reddening in our inner part.
) values remain within model values for stars with high metallicity in the inner part and low metallicity in the outer part this means that dust is probably not dominating the reddening in our inner part.




Next: Conclusions
Up: Vertical colour profiles &
Previous: Determining colour gradients
Contents
O.A. van den Berg
2006-09-05