



Next: Results & discussion
Up: Vertical colour profiles &
Previous: Creating colour profiles
Contents
Determining colour gradients
To determine colour gradients certain selections had to be made to decide which part of the colour profile we would fit. De Grijs & Peletier grijs2000 state that the total acceptable range for a gradient fit produces - in general - the most representative vertical colour gradients as a function of projected galactocentric distance: Any small-scale variations arising from excess out-of-plane extinction, foreground starlight or artefacts from low S/N ratios in the outer regions are smoothed out by using a relatively large vertical range.
The profiles were plotted to determine on which side the dust lane is lying (see Appendix C). This could easily be determined by the red peak of the central profile on the bulge. This was done to use the side of the profile that is least contaminated by dust extinction for the gradient fit, as it would create a systematic higher gradient, while we want to recover a gradient for which external effects by dust are minimized. By eye it was determined at which height a clear steep rise of the profile started and this point was used as a minimum height for all colour profiles of the galaxy. As the minimum scaleheight for most galaxies was around 1  , it was unnecessary to set a minimum depending on the scaleheight. We also wanted to be able to use as many datapoints possible.
, it was unnecessary to set a minimum depending on the scaleheight. We also wanted to be able to use as many datapoints possible.
The maximum height was determined by the ratio of 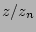 . This was set at 4.5
. This was set at 4.5  . A initial limit was set at a (
. A initial limit was set at a ( ) error larger than 0.1 mag to prevent erratic datapoints (very high or low values) to be taken into account. This limit already made most datapoints fall within the 4.5
) error larger than 0.1 mag to prevent erratic datapoints (very high or low values) to be taken into account. This limit already made most datapoints fall within the 4.5  limit, but this was not always sufficient as some remaining profiles still contained erratic datapoints. 4.5
limit, but this was not always sufficient as some remaining profiles still contained erratic datapoints. 4.5  is a typical limit also used in literature to mark the range of a qualitative good profile.
is a typical limit also used in literature to mark the range of a qualitative good profile.
The gradients of the profiles have to be matched to each other in case of radial variations so they contribute evenly to the determination of the central ( ) value. In the selected colour profiles we see no radial behaviour that would require a radial fit to correct the central (
) value. In the selected colour profiles we see no radial behaviour that would require a radial fit to correct the central ( ) value for each gradient. Without a radial behaviour the gradients are matched to each other by determining the average (
) value for each gradient. Without a radial behaviour the gradients are matched to each other by determining the average ( ) value of each cut at
) value of each cut at 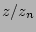 = 2. The deviation of (
= 2. The deviation of ( ) to the average (
) to the average ( ) at
) at 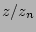 = 2 was then determined for each profile. With the already determined gradient value for each cut the correct (
= 2 was then determined for each profile. With the already determined gradient value for each cut the correct ( ) value at
) value at 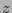 = 0 could be calculated for each cut and from this value the average. Too sustain the final colour we then correct for the galactic extinction to (
= 0 could be calculated for each cut and from this value the average. Too sustain the final colour we then correct for the galactic extinction to ( ). This is a constant value, but different for each galaxy, that has to be subtracted from the (
). This is a constant value, but different for each galaxy, that has to be subtracted from the ( ) value.
) value.
To determine the gradient the Levenberg-Marquardt linear least-squares algorithm was made to the selected profile, weighting the datapoints to their errors. The results of the ( ) colour gradients are determined in mag arcmin
) colour gradients are determined in mag arcmin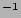 and in mag
and in mag 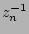 .
.




Next: Results & discussion
Up: Vertical colour profiles &
Previous: Creating colour profiles
Contents
O.A. van den Berg
2006-09-05