2D: Bessel function fitting

As a galaxy is not two dimensional but three dimensional a conversion between the face-on and edge-on galaxies is required to be able to use a similar description of the radial behaviour of the surface brightness. Van der Kruit vdkruit1979 showed that to keep the value of the scalelength that is determined for a face-on galaxy, which is derived from fitting an exponential function to the surface brightness, for an edge-on galaxy a modified Bessel function of the first order is required for the conversion, changing the fitting function to

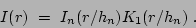$$I (r)\ =\ I_n (r/h_n) K_1 (r/h_n)\ .$$ (11)

The results from the line-of-sight integration assume a infinite disk without truncation. Truncation however, is a common feature of galaxies (see Kregel et. al. 2002 and Pohlen & Trujillo 2006) which makes the resulting scalelength from the Bessel function not exactly comparable to the face-on scalelength. The exponential radial function is just a simplified case which in practice works just as well. The new two dimensional two disk function, assuming no truncation, becomes

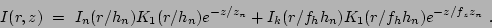$$I (r,z)\ =\ I_n (r/h_n) K_1 (r/h_n) e^{-z/z_n} + I_k (r/f_h h_n) K_1 (r/f_h h_n) e^{-z/f_{z} z_n}\ .$$ (12)

Computation times of either the exponential or the Bessel function proved to be similar, leaving us the freedom to choose either as the preferred fit function on that account.