



Next: 2D: Bessel function fitting
Up: Two dimensional (2D) disk
Previous: Two dimensional (2D) disk
Contents
2D: Exponential function fitting
The radial structure of a face-on galaxy can be described best by a broken exponential consisting of three distinct parts: the bulge, the inner disk and the outer disk. The bulge part is steep, the inner disk part much flatter, while the outer disk is often steep again. This latter kind of shape is called truncation (see figure 2 for an example). Each part has a different radial behaviour and one thus wants to avoid the bulge, as it is an additional component and may have a different vertical structure, and the outer disk, which has a different radial scalelength than the inner disk. The break points of the inner disk with the bulge and the outer disk were determined by eye, making sure points lying close to the break points were excluded. The inner disk, which we use to the fit, is described in the face-on case by the exponential function proposed by Freeman freeman1970 (see equation 2).
Adding this exponential radial fitting function to the 1D vertical fitting function creates a two dimensional fitting function which can be used as an extra constraint on possible varying radial behaviour of the inner surface brightness of the thin and the thick disk by combining all the cuts to obtain one set of fit values, i.e. there should be only one scaleheight for the thin and the thick disk at all radii.
As the thin and thick disk are assumed to have a constant  and
and 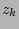 , their local
, their local 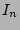 and
and 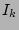 values are coupled by the radial distribution as a galaxy becomes fainter in its outer parts. As the scaleheights of the thin and thick disk are separate parameters, it is possible that the scalelengths of the thin and thick disk are different from each other. This requires the vertical functions of the two components to have a separate radial addition. We describe the scaleheight for the thick disk as a ratio factor
values are coupled by the radial distribution as a galaxy becomes fainter in its outer parts. As the scaleheights of the thin and thick disk are separate parameters, it is possible that the scalelengths of the thin and thick disk are different from each other. This requires the vertical functions of the two components to have a separate radial addition. We describe the scaleheight for the thick disk as a ratio factor
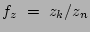 , to describe the difference between both scaleheights, leaving the thin disk scaleheight as the main scaleheight parameter. We did the same was for the scalelength, using the ratio
, to describe the difference between both scaleheights, leaving the thin disk scaleheight as the main scaleheight parameter. We did the same was for the scalelength, using the ratio
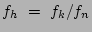 instead of
instead of 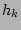 , leaving the thin disk scalelength as the main scalelength parameter. Using these factors makes it easier to assess our results. The new 2D fitting function becomes
, leaving the thin disk scalelength as the main scalelength parameter. Using these factors makes it easier to assess our results. The new 2D fitting function becomes
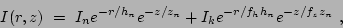 |
(10) |
where the thin disk scalelength 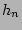 and
and 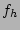 are two extra free parameter to the four existing free parameters, while the fit is done over
are two extra free parameter to the four existing free parameters, while the fit is done over 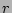 and
and 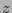 .
.




Next: 2D: Bessel function fitting
Up: Two dimensional (2D) disk
Previous: Two dimensional (2D) disk
Contents
O.A. van den Berg
2006-09-05