



Next: Vertical colour profiles &
Up: Discussion
Previous: Vertical structures revisited?
Contents
Comparison with literature
The main problem when comparing our results with literature is the wide variety in methods used to do the fits and hence obtain the thick disk parameters. Comparison of our results with literature is complicated, as few structure decompositions have been performed with some of them on the same galaxy and even fewer on late-type galaxies. We present the previous results in Table 17, which is adapted from Pohlen et al. (2004). 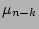 is also shown where possible to compare the faintness of the thick disk compared to the thin disk.
is also shown where possible to compare the faintness of the thick disk compared to the thin disk.
Our lower values for 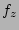 match previous found values, but our higher values exceed any previous values, although Morrison et. al. (1997) find a possible
match previous found values, but our higher values exceed any previous values, although Morrison et. al. (1997) find a possible 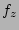 of 6.3 for NGC 891. The fact that the galaxy with our highest
of 6.3 for NGC 891. The fact that the galaxy with our highest 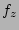 is also the galaxy in our sample with the most distinct thick disk component makes this extreme value hard to challenge. It also shows thick disks can be very flat and thus harder to distinguish from the background noise.
is also the galaxy in our sample with the most distinct thick disk component makes this extreme value hard to challenge. It also shows thick disks can be very flat and thus harder to distinguish from the background noise.
Our 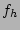 values give little rise to discussion as they are similar to previous results. Although we find some low and high values, these could be explained by the fit due to a possible coupling with
values give little rise to discussion as they are similar to previous results. Although we find some low and high values, these could be explained by the fit due to a possible coupling with 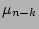 . Our
. Our 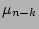 values encompass earlier results. The values from Pohlen et. al. (2004) are lower, but this could be caused by the different modelling method or the coupling effect of the fit. We also find several much larger
values encompass earlier results. The values from Pohlen et. al. (2004) are lower, but this could be caused by the different modelling method or the coupling effect of the fit. We also find several much larger 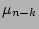 values. The only other result of such a large value is from Van Dokkum et. al. (1994). During our fits we noted that a
values. The only other result of such a large value is from Van Dokkum et. al. (1994). During our fits we noted that a 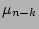 of 5.6 mag arcsec
of 5.6 mag arcsec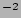 is an extreme maximum for the fit function with our surface brightness limit, and this kind of difference between surface brightness makes the fit degenerate as the fitting function can fit almost any thick disk scaleheight to such a larger difference in surface brightness if the thick disk is not as distinct as for NGC 5290. The low
is an extreme maximum for the fit function with our surface brightness limit, and this kind of difference between surface brightness makes the fit degenerate as the fitting function can fit almost any thick disk scaleheight to such a larger difference in surface brightness if the thick disk is not as distinct as for NGC 5290. The low 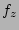 of Van Dokkum et. al. (1994) however, does not correspond to the typical degeneracy. They also used a 1D fit which showed in our tests to result in a larger
of Van Dokkum et. al. (1994) however, does not correspond to the typical degeneracy. They also used a 1D fit which showed in our tests to result in a larger 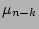 than the 2D fit and they used radially larger binned profiles to determine the fit, which could be of influence.
than the 2D fit and they used radially larger binned profiles to determine the fit, which could be of influence.
The use of radially larger binned profiles (this to increase the S/N ratio) than we did to determine vertical disk components is also used in Neeser et. al. (2002) and Abe et. al. (1999). Neeser et. al. (2002) first create many vertical bins with small equal widths and then average those in larger bins, with the bins growing larger over radius. Their summed bins are very large compared to our binsizes which we need to keep small to have sufficient cuts for a trustworthy 2D fit, where they use a 1D fit. Their low 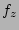 , in contrast to their high
, in contrast to their high 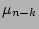 , makes the possible thick disk component seem hard to distinguish from the thin disk.
, makes the possible thick disk component seem hard to distinguish from the thin disk.
TABLE 17
L
ITERATURE T
HICK D
ISK R
ESULTS
| Galaxy |
Type |
Model |
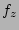 |
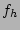 |
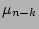 |
Reference |
| 11 galaxies |
Sb-Sc |
exp+exp |
3.3-7.7 |
0.6-3.4 |
3.4-5.6 |
This Study |
| 34 galaxies |
Sd |
sech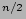 +sech +sech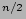 |
1.4-4.0 |
0.6-1.7 |
-0.8-3.5 |
YO06 |
| 5 galaxies |
S0 |
sech+sech |
2.6-5.3 |
1.7-1.9 |
2.2-3.0 |
PO04 |
| NGC 4710 |
S0 |
sech+exp |
3.2 |
|
|
DG96 |
| NGC 4762 |
S0 |
sech+exp |
4.6 |
|
|
DG96 |
| 5 galaxies |
S0 |
- |
1.8-4.6 |
|
|
DG97 |
| NGC 6504 |
Sab |
exp+exp |
4.0 |
|
5.6 |
VD94 |
| NGC 891 |
Sb |
exp+exp |
2.3-6.3 |
|
|
MO97 |
| NGC 891 |
Sb |
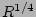 +sech +sech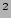 +exp +exp |
3.0 |
|
|
VA84 |
| NGC 4565 |
Sb |
sech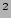 +sech +sech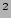 +halo +halo |
2.2 |
1.4 |
|
WU02 |
| NGC 4565 |
Sb |
sech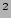 +sech +sech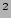 |
4.6 |
1.4 |
4.1 |
SH89 |
| NGC 4565 |
Sb |
exp+exp |
5.4 |
1.4 |
4.2 |
SH89 |
MW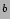 (optical) (optical) |
Sbc |
exp+exp |
3.0 |
1.3 |
|
LA03 |
MW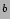 (NIR) (NIR) |
Sbc |
exp+exp |
3.3 |
1.3 |
|
OJ01 |
| ESO 342-017 |
Scd |
exp+exp |
2.5 |
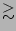 1.0 1.0 |
4.0-4.1 |
NE02 |
| IC 5249 |
Sd |
exp+exp |
3.0 |
0.6 |
|
AB99 |
Notes:  reference YO06: [Yoachim and Dalcanton2006], DG96: [De Grijs and Van der Kruit1996], DG97: [De Grijs and Peletier1997], VD: [Van Dokkum et al.1994], MO97: [Morrison et al.1997], VA84: [Van der Kruit1984], WU02: [Wu et al.2002], SH89: [Shaw and Gilmore1989], LA03: [Larsen and Humphreys2003], OJ01: [Ojha2001], NE02: [Neeser et al.2002], AB99: [Abe et al.1999]. reference YO06: [Yoachim and Dalcanton2006], DG96: [De Grijs and Van der Kruit1996], DG97: [De Grijs and Peletier1997], VD: [Van Dokkum et al.1994], MO97: [Morrison et al.1997], VA84: [Van der Kruit1984], WU02: [Wu et al.2002], SH89: [Shaw and Gilmore1989], LA03: [Larsen and Humphreys2003], OJ01: [Ojha2001], NE02: [Neeser et al.2002], AB99: [Abe et al.1999].  Milky Way. Milky Way. |
Abe et. al. (1999) used the same low-mass late-type galaxy (IC 5249) as we did, in the same band, using a 1D fit, so this provides a good comparison. However, we were unable to fit it in either a 2D or a 1D Two Disk fit. Abe et. al. (1999) however, use only 4 large radial bins for their fit and perform much larger conservative masking of stars than we did, which loss they correct by using large radial bins. Evenso, their 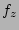 does not hint at the flat extended vertical structure we noticed. This difference could be caused by their conservative masking and by using large radial bins, something which we could do for a more extensive comparison. They find a
does not hint at the flat extended vertical structure we noticed. This difference could be caused by their conservative masking and by using large radial bins, something which we could do for a more extensive comparison. They find a 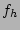 of 0.55, a value rather low and they are not hinting at the profound flatness we found (see Section 4.5). No thin and thick disk surface brightness is given so we cannot compare those. That they are able to fit this galaxy while we could not leaves the question of a possible thick disk component open for debate. We did not study the effect of these large radial bins, so we cannot say much about their effect on the vertical profile. It is possible they lost the vertical structure we noticed even in the vertical profiles of the original image. It might also be that the asymmetric shape of the galaxy caused our Two Disk fit to fail, which Abe et. al. (1999) solved by using large bins. However, the asymmetry is not an issue for FGC 2339.
of 0.55, a value rather low and they are not hinting at the profound flatness we found (see Section 4.5). No thin and thick disk surface brightness is given so we cannot compare those. That they are able to fit this galaxy while we could not leaves the question of a possible thick disk component open for debate. We did not study the effect of these large radial bins, so we cannot say much about their effect on the vertical profile. It is possible they lost the vertical structure we noticed even in the vertical profiles of the original image. It might also be that the asymmetric shape of the galaxy caused our Two Disk fit to fail, which Abe et. al. (1999) solved by using large bins. However, the asymmetry is not an issue for FGC 2339.
Yoachim & Dalcanton (2006) performed a 2D Two Disk fit, but used the sech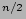 functions for their fits and their results originated from
functions for their fits and their results originated from 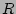 -band observations. While we fitted a large range of selected surface brightness profiles they fit the 2D Two Disk model on a cropped selection of the galaxy image without the use of any binning, fitting the model on each pixel of the image. This does mean that they keep a lower S/N ratio at higher scaleheights, while we try to increase the S/N in the outer parts by using growing bins to improve the quality of the fit, as this was necessary for us to be able to fit the vertical profiles. Another issue is their use of the Levenberg-Marquardt least-squares fitting which for us showed too many local minima and made it very difficult to determine what the global minimum is. However, they fitted in a completely different way, which makes it hard to compare, as we did not have galaxies from their sample. Yoachim & Dalcanton also show no vertical profiles to support the quality of their fit results, an important issue as we ourselves could find a succesful fit on NGC 1886, while there was no distinct thick disk component visible in the vertical profiles.
-band observations. While we fitted a large range of selected surface brightness profiles they fit the 2D Two Disk model on a cropped selection of the galaxy image without the use of any binning, fitting the model on each pixel of the image. This does mean that they keep a lower S/N ratio at higher scaleheights, while we try to increase the S/N in the outer parts by using growing bins to improve the quality of the fit, as this was necessary for us to be able to fit the vertical profiles. Another issue is their use of the Levenberg-Marquardt least-squares fitting which for us showed too many local minima and made it very difficult to determine what the global minimum is. However, they fitted in a completely different way, which makes it hard to compare, as we did not have galaxies from their sample. Yoachim & Dalcanton also show no vertical profiles to support the quality of their fit results, an important issue as we ourselves could find a succesful fit on NGC 1886, while there was no distinct thick disk component visible in the vertical profiles.
In our attempts to fit two late-type low-mass galaxies we clearly could distinct a vertical structure, but they did not resemble in any way the very small 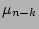 and
and 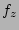 values that Yoachim & Dalcanton (2006) found. On the contrary. Our fits hint at a very flat vertical structure that hints of a long boxy structure like a ring or a large bar instead of a thick disk. They find 11 galaxies with a
values that Yoachim & Dalcanton (2006) found. On the contrary. Our fits hint at a very flat vertical structure that hints of a long boxy structure like a ring or a large bar instead of a thick disk. They find 11 galaxies with a 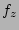 equal or lower to 2, and 18 galaxies between 2 and 3. Only four of their sample galaxies give an
equal or lower to 2, and 18 galaxies between 2 and 3. Only four of their sample galaxies give an 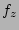 higher than 3. These values make it seem the thick disk is hard to distinguish from the thin disk. In their cases where the thick disk actually dominates the profile this structure should not be called a thick disk anymore if one considers the thick disk to be a faint extended component of the surface brightness profile. The small peak of the inner profile can be labelled to an inner disk or a young disk that is produced by enhanced star formation, with the outer part a more flatter or 'thicker' thin disk component.
higher than 3. These values make it seem the thick disk is hard to distinguish from the thin disk. In their cases where the thick disk actually dominates the profile this structure should not be called a thick disk anymore if one considers the thick disk to be a faint extended component of the surface brightness profile. The small peak of the inner profile can be labelled to an inner disk or a young disk that is produced by enhanced star formation, with the outer part a more flatter or 'thicker' thin disk component.
The best way to understand the effect of the different fitting methods is to perform all those methods on a large sample and compare the results. However, we limited ourselves to the different models and used the method we considered to provide the most accurate results. We showed the 1D Two Disk fit results to be similar to the 2D Two Disk fit results where the 2D fit provided a higher accuracy although it is more sensitive to strong irregularities. The 1D fit requires sufficient good profiles fitted to acquire good average parameter values, but in contrast to the 2D fit shows insight to the intrinsic properties and the true radial variation of each profile.




Next: Vertical colour profiles &
Up: Discussion
Previous: Vertical structures revisited?
Contents
O.A. van den Berg
2006-09-05