1D: Alternative fitting function fits to artifical galaxies

Tables 14 and 15 A1-A2 and B1-B2 show the results of the 1D profile fits with the weighted and an unweighted Generalized Gaussian and Sérsic Law respectively. The artificial galaxy for the fit has the input parameters $\mu_{n-k}$ = 3, $f_h$ = 2.0 and $f_z$ = 4.0, with a truncation at 2.5$h_n$, depicting an ideal thick disk galaxy. Two $\mu_0-\mu_\textrm{\scriptsize cut}$ values are used: 7.4 and 8.4 mag arcsec$^{-2}$. We do this to compare the behaviour of the fit for different depths. $\mu_0$ is the central surface brightness.
What you see immediately is that there is rarely any difference between the $\chi^2$'s of both methods, showing they fit evenly well and that using either model suffices with the main differences the parameter results. There are significant differences between the $z_0$ values of the weighted and the unweighted Generalized Gaussian. A similar thing can be said for the Sérsic Law. At $\mu_0-\mu_\textrm{\scriptsize cut}$ = 7.4 the Sérsic Law shows a typical growing trend of a larger scaleheight with radius, as expected from the thick disk's larger scalelength. At $\mu_0-\mu_\textrm{\scriptsize cut}$ = 8.4 however, the scaleheight is decreasing with radius. There are also notable differences between the results of the weighted and the unweighted fit, which would not have been expected, as the artificial galaxies provide smooth profiles that are easy to fit. A profile and fit with the weighted Generalized Gaussian is shown in figure 8, A profile and fit with the weighted Sérsic Law is shown in figure 9. Both have $\mu_0-\mu_\textrm{\scriptsize cut}$ set at 7.4 mag arcsec$^{-2}$. In the inner part a stronger up-bending can been seen, while both fitting functions cannot reproduce the bending to the thick disk component very well.

Figure 8: Fit with the Generalized Gaussian to an artifical galaxy.

Figure 9: Fit with the Sérsic Law to an artifical galaxy.

TABLE 14

1D WEIGHTED ALTERNATIVE FITTING FUNCTION RESULTS

A1: WEIGHTHED GENERALIZED GAUSSIAN [#MATH266# = 7.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
(1)	(2)	(3)	(4)	(5)
0.1392	41.0	16.98	3.16	0.53
0.1342	46.0	17.11	3.42	0.53
0.1301	52.0	17.19	3.40	0.53
0.1244	58.0	17.30	3.42	0.53
0.1134	64.0	17.44	3.62	0.54
0.1081	70.0	17.55	3.63	0.53
0.1023	77.0	17.68	3.65	0.53
0.0959	85.0	17.82	3.67	0.53
0.0850	93.0	18.02	3.90	0.53

B1: WEIGHTHED SÉRSIC LAW [#MATH267# = 7.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
(6)	(7)	(8)	(9)	(10)
0.1383	41.0	15.95	33.47	1.86
0.1342	46.0	16.03	33.99	1.87
0.1296	52.0	16.11	34.60	1.88
0.1244	58.0	16.21	35.29	1.89
0.1134	64.0	16.35	35.46	1.86
0.1081	70.0	16.46	36.30	1.87
0.1023	77.0	16.59	37.26	1.88
0.0959	85.0	16.74	38.36	1.89
0.0850	93.0	16.93	38.99	1.87

A2: WEIGHTHED GENERALIZED GAUSSIAN [#MATH268# = 8.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
0.1669	41.0	16.97	3.01	0.52
0.1635	46.0	17.06	3.11	0.53
0.1635	52.0	17.15	3.11	0.53
0.1636	58.0	17.27	3.18	0.53
0.1581	64.0	17.39	3.26	0.53
0.1581	70.0	17.51	3.26	0.53
0.1581	77.0	17.64	3.26	0.53
0.1507	85.0	17.82	3.44	0.54
0.1507	93.0	17.99	3.44	0.54

B2: WEIGHTHED SÉRSIC LAW [#MATH269# = 8.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
0.1669	41.0	15.88	33.03	1.91
0.1635	46.0	15.98	32.77	1.90
0.1635	52.0	16.07	32.77	1.90
0.1635	58.0	16.17	32.77	1.90
0.1581	64.0	16.30	32.41	1.87
0.1581	70.0	16.42	32.41	1.87
0.1581	77.0	16.55	32.41	1.87
0.1507	85.0	16.74	31.96	1.84
0.1507	93.0	16.90	31.96	1.84

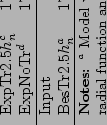
Notes: (1)(6) See Section 3.6 for the defitinion. (2)(7) Radial position of the profile. (3)(8) Central surface brightness. (4) Width of the distribution. (5) Shape parameter. (9) Halflight radius. (10) Power law index.

TABLE 15

1D UNWEIGHTED ALTERNATIVE FITTING FUNCTION RESULTS

A1: UNWEIGHTHED GENERALIZED GAUSSIAN [#MATH270# = 7.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
0.4426	41.0	16.45	1.44	0.44
0.4204	46.0	16.54	1.47	0.44
0.3964	52.0	16.65	1.51	0.44
0.3704	58.0	16.77	1.56	0.45
0.3390	64.0	16.93	1.71	0.45
0.3139	70.0	17.07	1.77	0.45
0.2875	77.0	17.22	1.84	0.45
0.2602	85.0	17.40	1.92	0.45
0.2289	93.0	17.62	2.12	0.46

B1: UNWEIGHTHED SÉRSIC LAW [#MATH271# = 7.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
0.4426	41.0	15.36	36.18	2.25
0.4204	46.0	15.45	36.79	2.25
0.3964	52.0	15.56	37.48	2.25
0.3704	58.0	15.68	38.27	2.25
0.3390	64.0	15.85	38.71	2.21
0.3139	70.0	15.98	39.66	2.21
0.2875	77.0	16.14	40.73	2.20
0.2602	85.0	16.31	41.93	2.20
0.2289	93.0	16.54	42.88	2.17

A2: UNWEIGHTHED GENERALIZED GAUSSIAN [#MATH272# = 8.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
0.5255	41.0	16.35	1.25	0.44
0.5252	46.0	16.42	1.23	0.43
0.5252	52.0	16.51	1.23	0.43
0.5252	58.0	16.61	1.23	0.43
0.5235	64.0	16.73	1.27	0.44
0.5235	70.0	16.85	1.27	0.44
0.5235	77.0	16.98	1.27	0.44
0.5150	85.0	17.18	1.36	0.44
0.5150	93.0	17.34	1.36	0.44

B2: UNWEIGHTHED SÉRSIC LAW [#MATH273# = 8.4]
	[$''$]	[mag/$\Box ''$]	[$''$]
0.5255	41.0	15.26	34.72	2.29
0.5252	46.0	15.33	34.75	2.30
0.5252	52.0	15.42	34.75	2.30
0.5252	58.0	15.52	34.75	2.30
0.5235	64.0	15.65	34.65	2.29
0.5235	70.0	15.77	34.65	2.29
0.5235	77.0	15.90	34.65	2.29
0.5150	85.0	16.09	34.38	2.26
0.5150	93.0	16.26	34.38	2.26

Notes: See Table 15 for a description