1D: Alternative fitting functions

As we are looking for an extended vertical structure next to the thin disk we expect not to be able to fit our profiles well with a two parameter fitting function as it will need to choose an intermediate solution that will not describe the shape of the profile sufficiently. The four parameter fitting function of the two disk (thin+thick) fit is not very stable and depends highly on the quality of the profile. A single fitting function that forms an intermediate solution between the one and two disk fit is the Sérsic Law, which is defined as

$$I(z)\ =\ I_0 \exp \left[-\kappa(n) \left[-(r/r_c)^{1/n}-1\right]\right] ,$$ (7)

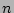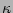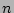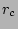where $n$ is the power law index with $\kappa$ depending on $n$ and $r_c$ is the halflight radius. There is no exact definition of 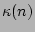$\kappa(n)$, so we use here the one determined by Balcells et al. balcells2001, which defines 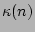$\kappa(n)$ as

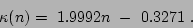$$\kappa(n) =\ 1.9992n\ -\ 0.3271\ .$$ (8)

There also exists a simplified version of the Sérsic Law which is called the Generalized Gaussian, which is defined as

$$I(z)\ =\ I_0 \exp \left[-(\vert r\vert/r_0)^{\lambda}\right] ,$$ (9)

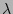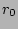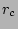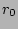where $\lambda$ is called the the shape parameter and $r_0$ the width of the distribution. The $r_c$ and $r_0$ in both functions are not the same and need to be converted for comparison. The keypoint is that both functions have 3 parameters, whereas the two and one disk fits have 4 and 2 respectively.