1D: Single disk model

A large family of fitting functions (see equation 3) is available to describe the behaviour of the vertical structure of an edge-on galaxy. As fitting for 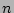$n$ adds in an extra and complex parameter to the fit, we have to choose a function to use for our fits. The exponential and the sech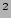$^2$ function are the two extremes within which those fitting functions behave. In the past both functions have been used to fit vertical surface brightness profiles and no clear preference has been decided on. This is because the main difference between sech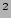$^2$ and exponential is only the inner part close to the plane. In the outer part both functions have the same shape. The sech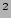$^2$ is thus mainly used to describe the inner part of the profile in case it shows intrinsic flattening (see figure 3 for an example), while the exponential function expects a peak.
Abe et al. abe1999 state that there is no need to use for a sech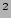$^2$ function to fit the vertical surface brightness profile they observed for IC 5249. The flattening in this case is not intrinsic to the galaxy but caused by external effects: seeing, the dustlane and a not exact inclination of 90$^{\circ}$.
Seeing is a common known flattening effect immediately caused by the observations. To determine up to where this flattening still influences the profile a preliminary fit in the 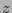$z$-direction was first made in a cut on a radial position that showed a clear flattened behaviour in the inner part so that a first approximation of where the flattening takes place could be made. The inner points were then removed and a fit was made to obtain the best starting values for the fit. The fitted curve was then convolved with a Gaussian filter to simulate the atmosphere's effect (matched to two times the FWHM), and plotted over the data set including the inner data points and the fitted curve. The point where the Gaussian filtered fitted curve broke away from the fitted curve could be taken as the boundary point where the seeing had too much influence over the dataset.
The flattening of the surface brightness profile is also caused by the remaining dustlane, which, especially in the J-band, absorbs part of the light. We could not distinguish its effect on the flattening from the effect of the seeing. Because we average over four quadrants for our two dimensional fits (see Section 3.4) we lose the advantage of taking the side with the least dustlane influence for the fit, especially when the galaxy is not perfectly edge-on, which is the case for most of our galaxies. The vertical size of the dustlane was determined by comparing the subtracted profiles of the original image with the average image.

Figure 4: Vertical profiles of observed artificial 3D galaxies at different inclinations. Each panel shows profiles at three different radii of a galaxy at 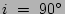$i\ =\ 90^{\circ }$ (left panel), 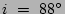$i\ =\ 88^{\circ }$ (middle panel), 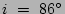$i\ =\ 86^{\circ }$ (right panel).

A third flattening effect happens when the galaxy is not exactly at an inclination of 90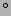$^{\circ}$. Figure 2 shows this effect for three different inclinations in a simple 3D exponential galaxy model with line-of-sight integration over the radius to create the 2D image. The same binning algorithm for our sample galaxies is also applied to show small effects, including a flattening of the inner region because of the binning. At 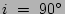$i\ =\ 90^{\circ }$ the profiles show a straight peak in the center, but the effects of the inclination grow rapidly at 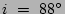$i\ =\ 88^{\circ }$ and even worse at 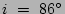$i\ =\ 86^{\circ }$, especially at larger radii, making it even harder to determine if a flattening is intrinsic or not.
To confirm that with our data we cannot tell where these effects disappear we would have to determine for each its boundary. As detailed deconvolution of the seeing is beyond the scope of this research and the inner flattened part we observed of no importance to our fitting we decided to use the exponential function and to remove all flattened inner points. We tested several of our sample galaxies on the effects of seeing and the dustlane and found them to be hard to distinguish from each other but always causing sufficient flattening that it was not possible to distinguish the observed from the intrinsic flattening.

After deciding on the exponential function, without an extra vertical structure component, only two parameters are needed to fit the vertical profile of a sample disk: the central intensity 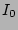$I_0$ and the scaleheight $z_0$,

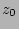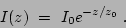$$I (z)\ =\ I_0 e^{-z/z_0}\ .$$ (4)

Since we fit the profile in magnitude arcsec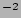$^{-2}$ even a simple linear fit would sustain when using an exponential function for the fit. The used function for this linear fit is

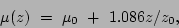$$\mu(z)\ =\ \mu_0\ +\ 1.086z/z_0 ,$$ (5)

where the factor 1.086 corrects for the exponential when the intensity is changed into a logarithmic surface brightness. This is the simplest way to fit the vertical distribution and we always apply it for comparison (see Appendix A).